Table of Content

ถ้าทุกคนต่างเห็นพ้องต้องกันหมดในเรื่องใดเรื่องหนึ่งเป็นเอกฉันท์ แสดงว่ามันต้องมีอะไรบ้างอย่างผิดปกติแล้วแหละ

Dec 26, 2021

Table of Content

ทุกคนต้องเคยแอบชอบใครจริงไหมครับ

สมมติว่าในห้องเรียนของนางสาวน้ำมีกันอยู่ 30 คน นางสาวน้ำกำลังแอบหลงรักนายโชนเข้า แต่เธอไม่รู้ว่านายโชนจะรักเธอตอบหรือไม่ นางสาวน้ำจึงตัดสินใจถามเพื่อนสนิทของเธอทีละคน

คนแรกคือท๊อป ท๊อปบอกว่า “พี่โชนต้องรักแกแน่เลยเว้ย”

คนที่สองคือเชียร์ เชียร์บอกว่า “พี่โชนเขาก็แอบเหล่มึงมาต้องนานแล้วว่ะ”

คนที่สามคือกี้ กี้บอกว่า “ไปบอกรักเลยเว้ย เขาน่ะแอบชอบเธอกลับมาตั้งนานแล้ว”

หากจะตั้งโจทย์คณิตศาสตร์เกี่ยวกับเรื่องนี้ คงอยากจะถามว่า ถ้าโอกาสที่พี่โชนจะรักนางสาวน้ำกลับนั้น มีโอกาสเพียงครึ่งต่อครึ่ง และถ้าเพื่อนแต่ละคนของนางสาวน้ำต่างก็จริงใจกับนางสาวน้ำด้วยกันทั้งหมด (ไม่มีใครมี conflict of interest กับความรักที่นางสาวน้ำมีต่อพี่โชน) แต่เรื่องของเรื่องคือไม่มีใครหรอกที่สามารถเดาใจคนอื่นได้ สมมติว่าโอกาสที่เพื่อนแต่ละคนของนางสาวน้ำจะเดาใจพี่โชนผิดนั้นมีประมาณ 10% ถามว่า

1. คิดว่า ถ้าสมมติว่าทุกคนที่นางสาวน้ำถามต่างก็อวยว่าความรักของนางสาวน้ำจะประสบความสำเร็จ นางสาวน้ำควรจะถามเพื่อนเรื่องนี้สักกี่คน ก่อนที่จะไปบอกรักกับพี่โชนเสียที
2. คิดว่าถ้าเพื่อนทั้งห้อง (28 คน ยกเว้นพี่โชนกับนางสาวน้ำ) บอกว่าพี่โชนแอบชอบนางสาวน้ำเหมือนกันทั้งหมด โอกาสที่โชนจะแอบชอบนางสาวน้ำจะกลายเป็นเท่าใด

คำตอบแรกคือ 3 คน (ถ้านางสาวน้ำหยุดถามที่กี้ โอกาสที่พี่โชนจะชอบน้ำจริง ๆ จะ max สุดตรงนี้ คือประมาณ 80%)

คำตอบที่สองคือ โอกาสที่พี่โชนจะชอบนางสาวน้ำจริง ๆ จะเหลือแค่ 50% นิด ๆ (ซึ่งหมายความว่า นางสาวน้ำเสียเวลาอย่างมากในการถามคนอื่นถึง 28 คน เพราะถึงจะไม่ถามใครเลยก็มีโอกาส 50% อยู่ดี)

นอกจากนั้น ยังพิสูจน์โดยใช้ Bayesian Statistics ได้อีกด้วยว่า หลังพ้นจากการถาม 3 คนนั้นไปแล้ว โอกาสที่พี่โชนจะรักนางสาวน้ำจริง ๆ จะเริ่มน้อยลง ถ้ามีเพื่อนคนที่ 4 และที่ 5 และที่ 6 ต่างก็มาอวยความรักของนางสาวน้ำเรื่อย ๆ

เรื่องนี้ดู make sense อย่างมากเมื่อพูดคุยในมุมของของเรื่องรักวัยเรียน แน่นอนว่าถ้าเพื่อนทุกคนอวยนางสาวน้ำในเรื่องที่ว่าพี่โชนจะต้องชอบนางสาวน้ำกลับแน่ ๆ แล้ว แสดงว่าไม่มีใครเลยที่น่าไว้ใจ เพราะทุกคนพูดเหมือนกันทั้งหมด แต่ถ้าเกิดว่าเมื่อใดก็ตามที่มีใครสักคนหรืออาจจะสองคน ที่บอกกับนางสาวน้ำว่า “คนอย่างเอ็ง พี่โชนเค้าไม่เอาหรอก” แล้ว ถึงแม้ว่านั้นจะทำให้โอกาสที่พี่โชนรักนางสาวน้ำนั้นลดลงไปบ้าง (เสียใจด้วยนะน้ำ) แต่ก็จะทำให้ค่ารับรู้โอกาสของน้ำ ตรงกับความเป็นจริงมากขึ้น (ซึ่งนั่นเป็นเรื่องที่ดี)

การที่มีคนมา confirm ในเรื่องเดียวกันทุกคน แต่ทำให้เรื่องนั้นมีโอกาสที่จะเป็นจริงน้อยลงเรื่อย ๆ เรียกกันแบบบ้าน ๆ ว่า The paradox of unanimity (ปฏิทรรศน์แห่งความเป็นเอกฉันท์)

เรื่องนี้ไม่ใช่เรื่องเล่น ๆ แต่เป็นเรื่องที่ค่อนข้างจริงจังมานับตั้งแต่สมัยโบราณกาลแล้ว ในระบบศาลของชาวยิว หากการตัดสินคดีใดที่ผู้พิพากษาต่างเห็นพ้องต้องกันด้วยกันทั้งหมด จำเลยในคดีนั้นจะถูกปล่อยตัวไปเลย

ในทางนิติวิทยาศาสตร์ก็มีเรื่องนี้เข้ามาช่วยในการตัดสินใจเช่นกัน ยกตัวอย่างเช่น การให้ผู้ต้องหาในคดีหนึ่ง ๆ มายืนเรียงกันแล้วให้พยานชี้คนผิดนั้น หากพยานสามารถเห็นผู้กระทำผิดได้อย่างชัดเจนในคดีก็คงไม่มีปัญหามากนัก แต่ประเด็นของเรื่องนี้คือ หากช่วงที่เกิดคดี พยานไม่สามารถเห็นผู้กระทำผิดอย่างชัดเจน แล้วในตอนที่ชี้ตัวนั้น พยานต่างเห็นพ้องต้องกันว่าผู้กระทำผิดน่าจะเป็นคนนั้นคนนี้ ถ้าโอกาสที่พยานจะชี้ตัวผิดมี 1\% (เท่ากับตัวอย่างที่แล้ว) และพยานมีสิบปากที่บอกอย่างเป็นเอกฉันท์ว่าคนเดียวกันนี้แหละที่เป็นผู้กระทำผิด โอกาสที่คนนั้นจะผิดจริงจะเหลือแค่ 60\% และถ้าเกิดว่าเราต้องการให้ค่านั้นสูงถึง 95\% (มีความผิดพลาด 5\% ที่อาจยอมรับได้) ค่า 60\% นั้นแทบจะเอามาใช้ในกระบวนการยุติธรรมไม่ได้เลย

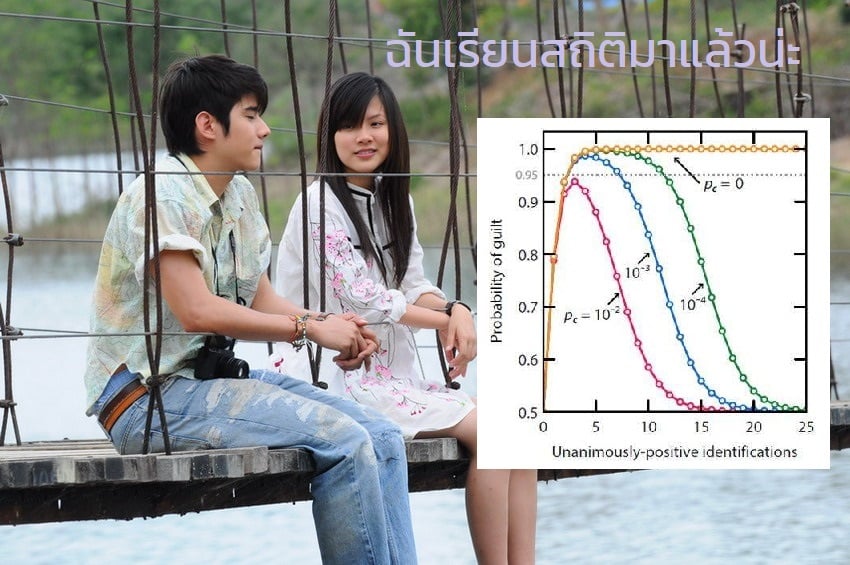
จากกราฟในภาพดังแนบ เป็นการพล็อตระหว่างจำนวนคนที่เห็นพ้องต้องกันเป็นเอกฉันท์ (unanimously positive test) และโอกาสที่ผู้ที่ถูกกล่าวหาคนนั้นว่าเป็นผู้กระทำความผิด (possibility of guilt) ในกราฟมีค่าระบุ p_c คือค่าความผิดพลาดที่พยานชี้ตัวคนผิด (อาจจะเกิดจากภาพผู้ต้องหาไม่ชัด หรือการแบ่งแยกทางเพศ ชนชาติ สีผิว หน้าตา หรืออะไรก็แล้วแต่) ซึ่งจะเห็นได้ว่าในกรณีที่ p_c = 0 (พยานเห็นผู้กระทำผิดชัดเจน) การที่ยิ่งมีเสียงที่เป็นเอกฉันท์จะทำให้โอกาสที่ผู้นั้นเป็นคนผิดจริงจะมีมากขึ้นเรื่อย ๆ แต่ถ้าพยานเกิดไม่สามารถระบุตัวผู้ผิดอย่างแม่นยำ เมื่อเสียงที่เป็นเอกฉันท์เยอะมากขึ้นเรื่อย ๆ จะมีจุดหนึ่งที่โอกาสที่ผู้นั้จะเป็นคนผิดจริงจะเริ่มน้อยลง จนเข้าใกล้เคียงค่าเดิมตอนแรกที่ยังไม่ได้ถามพยานเลย

ปัญหาที่มาจาก Paradox of unanimity นั้นเกิดจากการที่เราต่างก็มีข้อผิดพลาดในการตัดสินใจด้วยกันทั้งหมด (p_c จะไม่เป็นศุนย์แน่นอน) เพราะฉะนั้นหากทุกคนเห็นพ้องต้องการในเรื่องต่าง ๆ อย่างเป็นเอกฉันท์ แสดงว่า

1. ความน่าไว้วางใจว่าผลลัพธ์นั้นมีค่าจริง ๆ (ไม่เอนเอียง ไม่เกิดจากการตอบตาม ๆ กัน ฯลฯ) จะมีค่าน้อยลง และ
2. โอกาสที่ความผิดพลาดจากผลลัพธ์นั้น (เช่น มีคนยัดใต้โต๊ะเพื่อให้มีการตัดสินใจตามที่คนยัดต้องการ หรือ การทดลองในแลปที่ผู้ทำการทดลองทำผิดแบบเดิม ๆ ซ้ำ ๆ โดยไม่รู้ตัว ฯลฯ) จะมีมากขึ้น

ตัวอย่างการประยุกต์ใช้ของ Paradox of unanimity ในชีวิตจริง เช่น

• เรื่องอื้อฉาวของ Volkswagen ในปี 2015 ที่หลอกค่าการปลดปล่อยมลพิษของรถด้วยการโปรแกรมชิปให้บอกผลแบบซ้ำ ๆ กัน แต่ผลมีค่าใกล้เคียงหลายครั้งมากจนผิดสังเกต ทำให้เกิดการสอบสวนอย่างหนักในหลายประเทศ จน CEO ของบริษัทในช่วงนั้นถูกจำคุก
• ตำรวจในยุโรปพบ DNA ของนางสาวคนเดียวกันในคดีฆาตกรรมถึง 15 คดีทั่วยุโรปในช่วงปี 1993 - 2008 จนถูกตั้งฉายาว่าเธอเป็น Phantom of Heilbronn โดยตำรวจไม่สามารถสาวหาเธอได้เลย จนสุดท้ายก็พบว่า DNA ของเธอนั้นความจริงแล้วมาจากเจ้าหน้าที่คนเดียวกันที่ทำหน้าที่อย่างสะเพร่า

เรื่องนี้สอนให้รู้ว่าอะไร

• หากการประชุมมีเสียงแตกจากเสียงส่วนใหญ่ ให้ขอบคุณพระเจ้าว่าการประชุมนั้นจะเป็นการประชุมที่มีค่าอย่างมาก เพราะจะทำให้การตัดสินใจขององค์กรดีขึ้นกว่าการประชุมที่มีมติเป็นเอกฉันท์ ซึ่งมักจะมีความเสี่ยงอย่างมากที่การตัดสินใจนั้นเกิดจาก bias ของแต่ละคน
• ถ้าเพื่อนทุกคนในกลุ่มต่างก็สนับสนุนให้เราทำสิ่งใดสิ่งหนึ่งด้วยเหตุผลบางประการ แต่แล้วก็มีเพื่อนอีกคนที่มาเตือนว่าอย่าหาทำ ถึงแม้จะเป็นแค่คนเดียวแต่ให้ฟังเขาด้วยน้ำหนักที่มากกว่าปกติ
• เวลาจะบอกรักใครสักคน ไม่ต้องถามคนทั้งห้องว่าเราควรบอกรักเขาหรือเธอไหม เพราะไม่มีใครที่รู้ใจของเขาหรือเธอคนนั้นหรอก นอกจากตัวของเขาหรือเธอคนนั้นเอง… (จบ)